Lohnt sich die Dämmung der obersten Geschossdecke?
Seit Oktober 2022 habe ich die oberste Geschossdecke meines Walmdach-Bungalows gedämmt. Hier erfahrt ihr, was es gebracht hat - und was es alles so auszuwerten gibt.
Stichprobe Oktober bis Dezember
Seit 2019 protokolliere ich den Gasbedarf des Hauses auf Monatsbasis. Jetzt im Januar kann ich daher sinnvoll die Zeit Oktober-Dezember mit den Vorjahren vergleichen:
| Jahr | Gasbedarf ∑Oct-Dec |
|---|---|
| 2019 | 9324kWh |
| 2020 | 9497kWh |
| 2021 | 9350kWh |
| 2022 | 4588kWh |
Für die Jahre 2019-2021 ergibt sich ein Durchschnittswert von 9396kWh für die drei Monate. Die 4588kWh von 2022 sind damit 48,82% des Vorjahreswertes - oder eine Reduzierung von 51,12%. Dies übertrifft die Reduzierung von 30-40% aus meiner Heizlastberechnung deutlich.
Ein detaillierterer Vergleich
Um saisonale Effekte auszuschließen (“warmer Winter” / “kalter Winter”), können die Daten auch mit Bezug auf die Monatsdurchschnittstemperatur betrachtet werden. Hier zeigt sich, dass zwar der Oktober 2022 der wärmste Oktober meiner Aufzeichnungen ist - der November 2022 war aber ebenso warm wie der November 2020 und der Dezember 2022 sogar 1-2°C kälter als die Dezember der Vorjahre.
Im Schnitt wurden jeden Monat 1500kWh weniger Heizwärme benötigt, die Visualisierung zeigt das auch sehr eindrücklich:
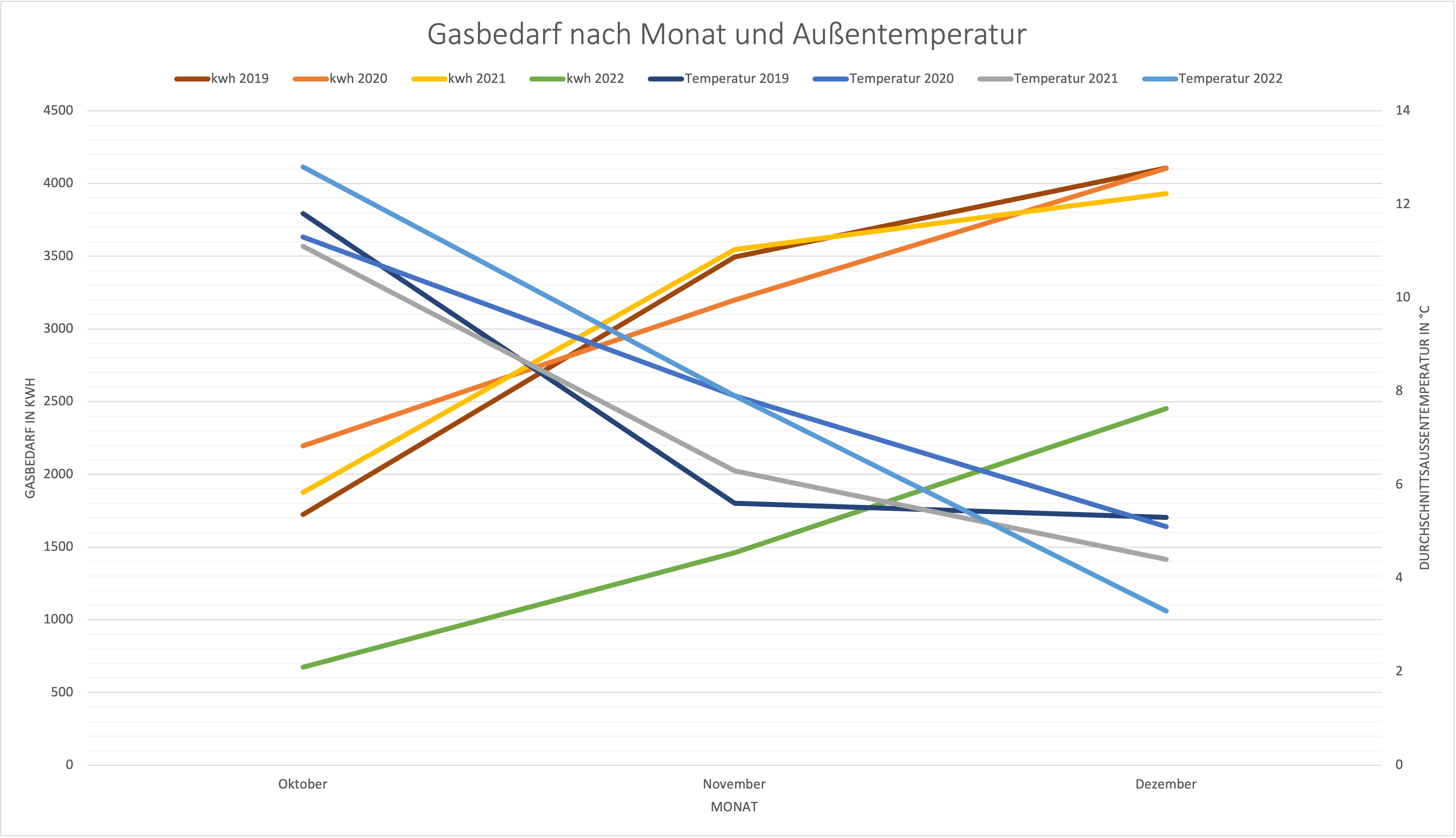
Noch etwas mehr im Detail
Durch den smarten Gaszähler kann die Auflösung der Analyse noch weiter erhöht werden. Die folgende Grafik zeigt die Tagesmitteltemperaturen und den Gasverbrauch des jeweiligen Tages. Zu erwarten wäre, dass der Gasverbrauch an kälteren Tagen höher ist als an warmen Tagen.
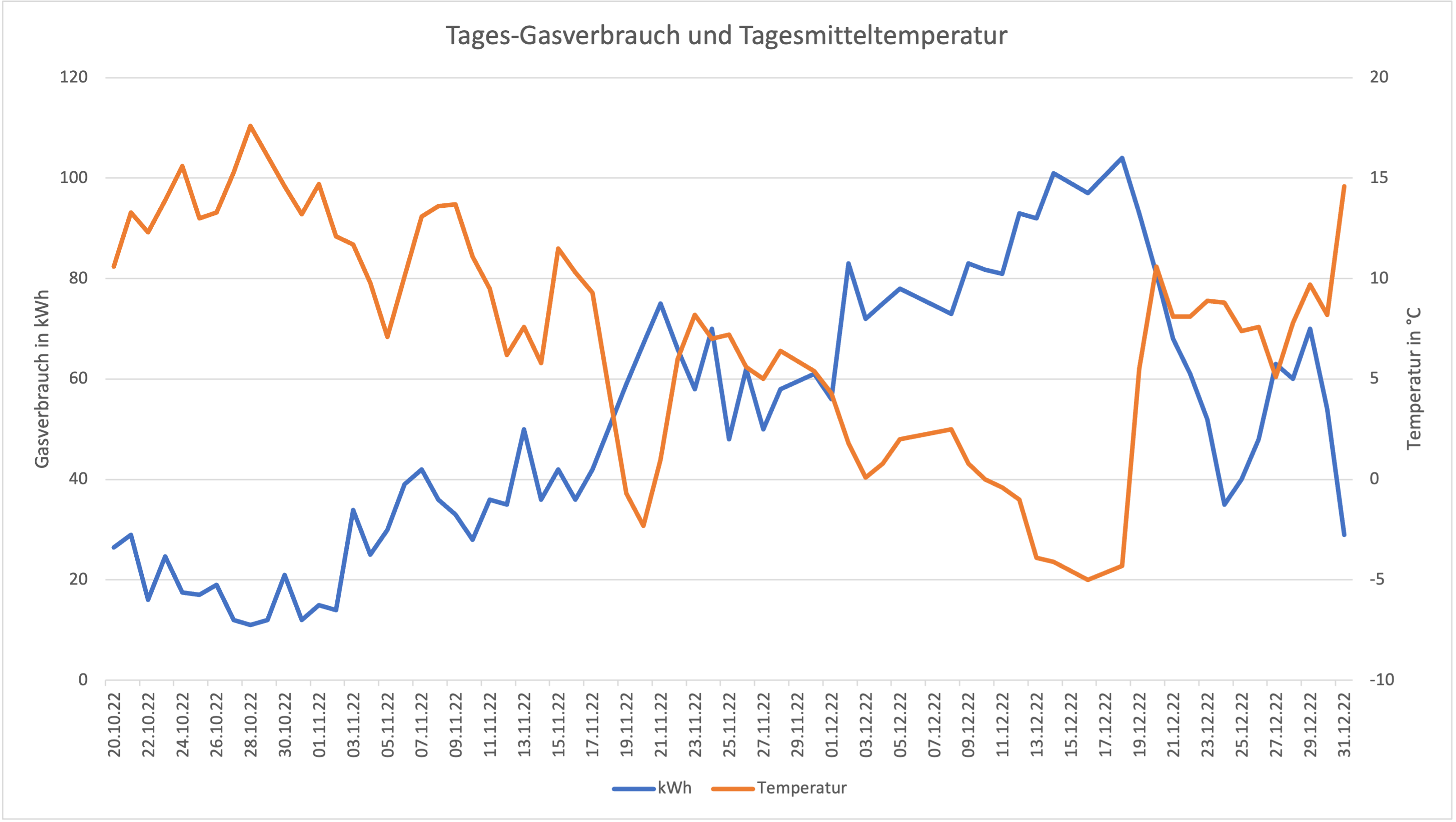
Dies ist grundsätzlich auch der Fall, die beiden Linien laufen einander entgegengesetzt. Es gibt allerdings auch Ausnahmen - so sind vom 05.11 auf den 07.11 Temperatur und Gasverbrauch angestiegen, ähnliches ist am 13.11. zu beobachten. Eine mögliche Erklärung könnte erhöhter Warmwasserverbrauch durch bspw. Baden sein - aber auch Tage an denen einzelne Räume höher geheizt wurden weil bspw. im Home Office gearbeitet wurde. Am 24.12 ist ferner zu sehen, dass trotz näherungsweise gleichbleibender Außentemperatur der Gasverbrauch erheblich gesunken ist - eventuell war an diesem Tag ausnahmsweise der Holzofen in Betrieb ;-).
Auch wenn der Zusammenhang zwischen Außentemperatur und Gasbedarf letztlich offenkundig ist, zeigt die Grafik doch sehr plastisch, wie direkt dieser Zusammenhang letztlich auch ist - es gibt bspw. keine größeren Verzögerungen.
Ein Heizwärme-Modell für mein Haus
Mit diesem Wissen bietet es sich an, ein Modell zu entwerfen, das saisonale Effekte ausmittelt und mir auch in Zukunft verrät, mit welchem Heizwärmebedarf ein vergleichbarer Monat im ungedämmten Zustand zu Buche geschlagen hätte.
Unten stehende Grafik zeigt ein entsprechendes Modell:
- In blauen Punkten ist der jeweilige Heizwärmebedarf im ungedämmten Zustand bei einer gegebenen Monatsdurchschnittstemperatur aufgezeigt
- In roten Kreuzen ist der Heizwärmebedarf im gedämmten Zustand aufgezeigt
- Die gepunkteten Linien stellen die dazugehörigen Regressionsmodelle dar
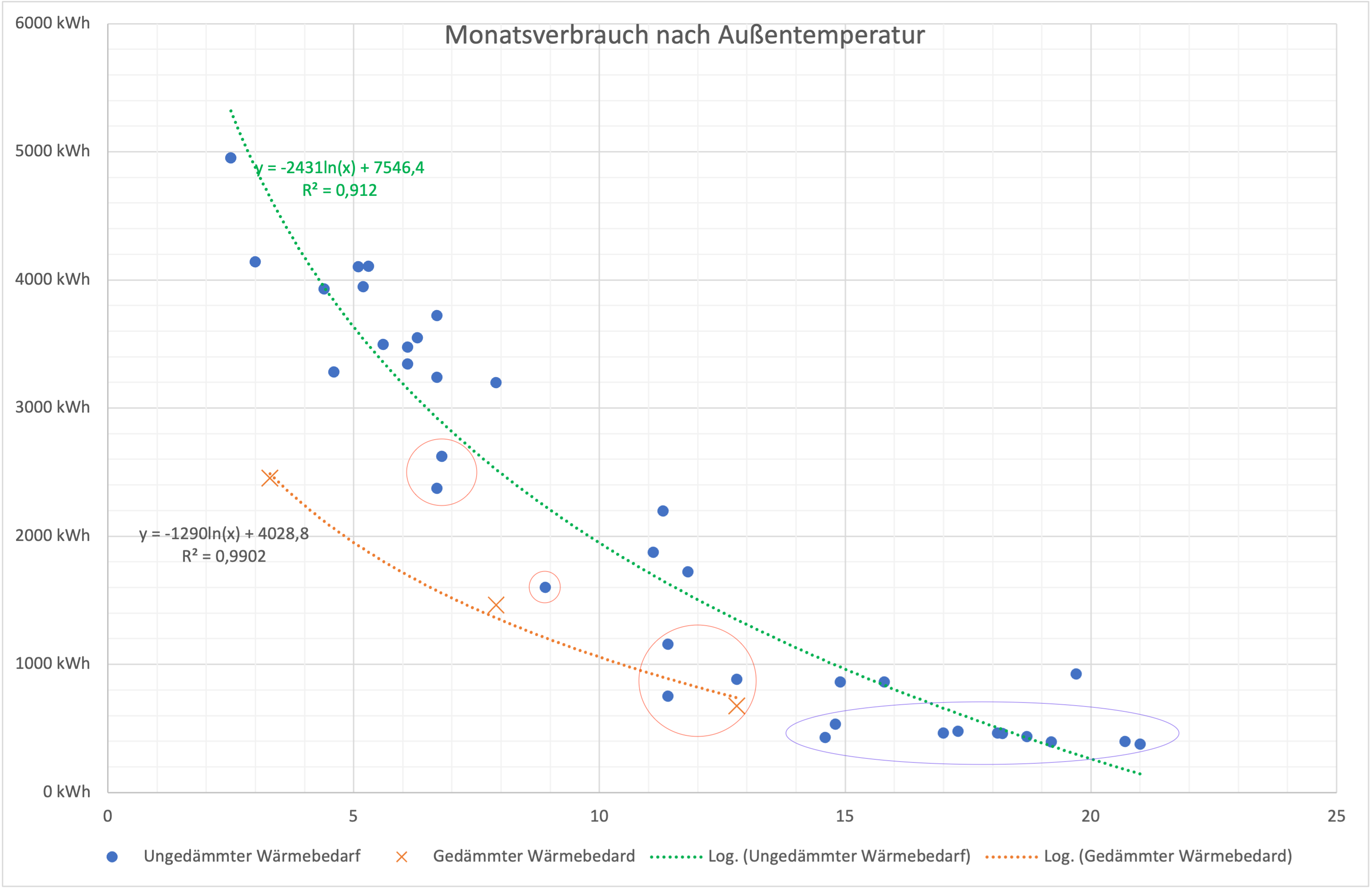
Auch in diesem Chart ist deutlich zu erkennen, dass der Heizwärmebedarf erheblich geringer ist. Je geringer die Außentemperatur, desto höher die Einsparung - die Graphen laufen erkennbar nach links auseinander.
Erste Beobachtung: Im Temperaturbereich 8°C aufwärts erscheinen die Unterschiede weniger deutlich - hier gibt es auch im ungedämmten Zustand einige Datenpunkte, die den gedämmten Werten sehr nahe kommen (bspw. bei 11,4°C). Warum ist das so? Tatsächlich gibt es hier eine kleine Besonderheit: Die blauen Datenpunkte die in diesem Temperaturbereich unterhalb der Trendlinie des ungedämmten Zustandes liegen (mit rotem Kreis markiert), stammen ausschließlich aus dem Frühjahr. Eine mögliche Erklärung wäre ein gewisser “Frühjahrseffekt”, bei dem bei steigenden Temperaturen das Heizen schneller eingestellt wird, wohingegen im Herbst bei fallenden Temperaturen vielleicht schneller zum Thermostat gegriffen wird. Selbst wenn also scheinbar der Oktober-Wert des gedämmten Gebäudes nur unwesentlich geringer ist als einige Vorjahreswerte: Tatsächlich liegt der Oktober damit deutlich unter allen vergleichbaren Herbst- und Wintermonaten und gleichauf mit den Frühjahrsmonaten mit ihren eher geringen Heizwärmebedarfen bei gleicher Durchschnittsaußentemperatur.
Zweite Beobachtung: Ab etwa 14°C Monatsdurchschnittstemperatur scheint der Heizwärmebedarf sich bei um die 400kWh einzupegeln (blaues Oval). Da dieser Wert von 400kWh auch im Hochsommer nicht unterschritten wird, dürfte es sich hierbei um die zur Trinkwassererwärmung benötigte Energie handeln. Der Wert erscheint mir relativ hoch - das schaue ich mir bei Gelegenheit nochmal genauer an. An diesen Werten lässt sich gleichzeitig die Heizgrenztemperatur des Hauses gut ablesen: Ab diesen Temperaturen scheint ein Beheizen des Hauses nicht mehr nötig zu sein. Dies deckt sich auch mit den viel zitierten 15°C die für ältere Gebäude oft angegeben werden. Die folgenden Jahre werden zeigen, ob auch die Heizgrenztemperatur durch die Dämmung deutlich gesenkt werden kann.
Dritte Beobachtung: Die Streuung der Datenpunkte beim ungedämmten Gebäude schlägt sich im Bestimmtheitsmaß R² nieder. Die Standardabweichung beträgt hier etwa 436kWh. Da die Stichprobe des gedämmten Gebäudes sehr gering ist, sieht das Bestimmtheitsmaß zwar besser aus - ist aber nicht aussagekräftig. Vergleicht man den Intercept der Regressionsmodelle, ist erkennbar, dass der Basisverbrauch des ungedämmten Gebäudes bei 1°C Durchschnittstemperatur 7546kWh beträgt - beim gedämmten Gebäude lediglich 4028kWh. Am Koeffizienten der Temperaturvariabel ist abzulesen, dass die Kurve insgesamt deutlich flacher verläuft (-2431ln(x) vs -1290ln(x)); Temperaturunterschiede wirken sich also auch deutlich weniger heftig aus. Beide Ergebnisse sind erwartbar - die beiden Regressionen im Vergleich zeigen aber wie sehr der Grundwärmebedarf (Intercept) und wie sehr die Temperaturabhängigkeit (Koeffizient der Variable X) gesunken sind.
Gibt es noch andere Faktoren?
Tatsächlich habe ich auch untersucht, ob man durch Hinzunahme weiterer Variablen die Genauigkeit des Modells noch verbessern kann. Hierzu habe ich meine Daten durch zusätzliche Wetterinformationen angereichert und die für mich eher uninteressanten Nicht-Heizmonate entfernt.
| Monat | Mit. Temp | Min. Temp | Max. Temp | ml Regen | Max Regen | Sonnenstd. | Sommertage | Heiße Tage | Frosttage | Streng Frost | Eistage | kwh |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2021/12 | 4,4 | -5,3 | 14,5 | 44 | 6,1 | 22,7 | 0 | 0 | 10 | 0 | 2 | 3929 |
| 2021/11 | 6,3 | -2,4 | 13,5 | 22,9 | 7 | 44,3 | 0 | 0 | 6 | 0 | 0 | 3546 |
| 2021/10 | 11,1 | 0,5 | 19,6 | 43,9 | 7,4 | 101,9 | 0 | 0 | 0 | 0 | 0 | 1874 |
| 2021/09 | 15,8 | 5,3 | 28,6 | 36,9 | 25,2 | 165,6 | 3 | 0 | 0 | 0 | 0 | 862 |
| 2021/03 | 6,1 | -5,6 | 24,5 | 41,7 | 7,7 | 129,6 | 0 | 0 | 9 | 0 | 0 | 3474 |
| 2021/02 | 3 | -17,3 | 19,1 | 56,1 | 15,2 | 101,1 | 0 | 0 | 12 | 6 | 7 | 4140 |
| 2021/01 | 2,5 | -5,3 | 12,4 | 72,3 | 11,8 | 28,7 | 0 | 0 | 14 | 0 | 0 | 4951 |
| 2020/12 | 5,1 | -1,3 | 13,7 | 68,6 | 13,7 | 25 | 0 | 0 | 4 | 0 | 0 | 4103 |
| 2020/11 | 7,9 | -5 | 19,9 | 39,9 | 8 | 91,1 | 0 | 0 | 5 | 0 | 0 | 3198 |
| 2020/10 | 11,3 | 1,7 | 20,1 | 75,7 | 12,4 | 51,1 | 0 | 0 | 0 | 0 | 0 | 2194 |
| 2020/09 | 14,9 | 5,1 | 31,5 | 38,2 | 21 | 192,2 | 5 | 1 | 0 | 0 | 0 | 862 |
| 2020/03 | 6,7 | -5,2 | 16,6 | 50,4 | 7,3 | 173,1 | 0 | 0 | 9 | 0 | 0 | 3237 |
| 2020/02 | 6,7 | -1,6 | 18,3 | 126,6 | 17,9 | 58,8 | 0 | 0 | 2 | 0 | 0 | 3721 |
| 2020/01 | 5,2 | -5,2 | 13,4 | 26,1 | 3,9 | 30,4 | 0 | 0 | 8 | 0 | 0 | 3948 |
| 2019/12 | 5,3 | -3,7 | 15,2 | 60,4 | 13,4 | 46,3 | 0 | 0 | 9 | 0 | 0 | 4107 |
| 2019/11 | 5,6 | -2,4 | 15,9 | 76,5 | 29 | 45,1 | 0 | 0 | 6 | 0 | 0 | 3495 |
| 2019/10 | 11,8 | -0,8 | 22,3 | 89,1 | 15,8 | 100,3 | 0 | 0 | 1 | 0 | 0 | 1722 |
Die Regressionsanalyse in Excel liefert hierfür dieses Ergebnis:
SUMMARY OUTPUT
Regression Statistics
Multiple R 0,997754325
R Square 0,995513693
Adjusted R Square 0,985643818
Standard Error 143,8192371
Observations 17
ANOVA
df SS MS F Significance F
Regression 11 22948918,91 2086265,356 100,8638601 3,84991E-05
Residual 5 103419,8648 20683,97296
Total 16 23052338,78
Coefficients Standard Error t Stat P-value Lower 95% Upper 95% Lower 95,0% Upper 95,0% Irrelevant
Intercept 5628,775833 431,929748 13,03169291 4,74551E-05 4518,465069 6739,086598 4518,465069 6739,086598
X Variable 1 -315,6428902 46,90816553 -6,728954046 0,001098815 -436,2241685 -195,061612 -436,2241685 -195,061612
X Variable 2 -16,98270191 47,23304287 -0,359551299 0,733869319 -138,399104 104,4337001 -138,399104 104,4337001 *
X Variable 3 5,054510558 20,18486151 0,25041096 0,812233556 -46,83232779 56,94134891 -46,83232779 56,94134891 *
X Variable 4 5,96373797 2,22102151 2,685132919 0,043551615 0,25442042 11,67305552 0,25442042 11,67305552
X Variable 5 -25,41915534 9,418446557 -2,698869201 0,042841916 -49,63004298 -1,208267695 -49,63004298 -1,208267695
X Variable 6 -3,336589275 1,517664226 -2,198502949 0,079243164 -7,237869367 0,564690816 -7,237869367 0,564690816 *
X Variable 7 379,9350393 127,5589321 2,978505957 0,030852997 52,03436534 707,8357132 52,03436534 707,8357132 **
X Variable 8 -1087,763338 376,873756 -2,886280407 0,03433546 -2056,548169 -118,9785062 -2056,548169 -118,9785062 **
X Variable 9 -1,914166837 27,328716 -0,070042326 0,946875044 -72,16486778 68,33653411 -72,16486778 68,33653411 *
X Variable 10 196,9525573 119,8702816 1,643047423 0,161294834 -111,1838113 505,0889258 -111,1838113 505,0889258 *
X Variable 11 -243,0691089 86,93884987 -2,795862946 0,038179595 -466,5525372 -19,58568062 -466,5525372 -19,58568062 **
Nun sieht der Wert für R² natürlich erstmal deutlich besser aus (99% im Vergleich zu den 91% zuvor). Hierzu gibt es aber einige Beobachtungen:
- Auch ohne Hinzunahme weiterer Variablen kann ich das Modell auf einen R-Wert von 93% bringen, wenn ich die Nicht-Heizmonate entferne.
- Üblicherweise werden Variablen mit einem P-Wert > 0,05 als nicht signifikant angesehen (oben mit * markiert). Da ein Modell mit vielen unnützen, schwer zu messenden Variablen natürlich wenig hilfreich ist, sollte diese Variablen entfernt werden
- Einige weitere Variablen wie “Sommertage”, “Heiße Tage”, “Eistage” haben zwar einen besseren P-Wert - sind aber mit so wenig Datenpunkten versehen, dass hier eine Überanpassung des Modells zu befürchten ist (oben mit ** markiert).
- Nimmt man all diese Variablen aus der Berechnung heraus, bleiben noch “ml Regen” und “Max Regen” übrig, das Modell hat aber “nur” noch einen R²-Wert von 97% (und zeigt für die beiden Regen-Variablen ebenfalls einen zu hohen P-Wert an). 4 Prozentpunkte mehr Genauigkeit im Vergleich zu dem um Sommertage bereinigten, allein auf Durchschnittstemperatur basierten Modell? Das ist den Aufwand nicht wert!
Was bringt mir das?
Grundsätzlich handelt es sich hierbei natürlich um eine Spielerei: Wieviel die Dämmung einspart sehe ich am Monatsende am Gaszähler und dass bei niedrigen Temperaturen mehr geheizt werden muss als bei hohen dürfte dem kundigen Beobachter auch vorher schon bewusst gewesen sein.
Dennoch erlaubt mir das Regressionsmodell dem aktuellen Heizwärmebedarf im gedämmten Zustand eine (halbwegs) belastbare, konkrete Zahl gegenüberzustellen, die ich sonst ggf. nicht hätte. So war beispielsweise der Dezember bis kurz vor Weihnachten außergewöhnlich kalt: Statt der sonst üblichen 3,5°C im Monatsmittel hatten wir zwischenzeitlich Durchschnittstemperaturen von unter 2°C. Das hätte im ungedämmten Zustand (nach dem Modell) zu 5867kWh Heizwärmebedarf geführt - und damit nochmal 1000kWh mehr als im bisher kältesten Monat meiner Aufzeichnungen.
Fazit: Dämmung
Wie schon eingangs erwähnt sieht es derzeit danach aus, dass die Dämmung eine Einsparung von etwa 52% im Vergleich zum Vorjahr ermöglicht. Gerade auch im anfänglich sehr kalten Dezember hat sich das bestätigt. Gleichzeitig ist anzunehmen, dass der Wert noch etwas sinkt - da in den Sommermonaten ausschließlich der Warmwasserverbrauch zu Buche schlägt - der durch die Dämmung natürlich nicht beeinflusst wird. Die Dämmung der obersten Geschossdecke dürfte sich bei Gaspreisen von derzeit 0,12ct/kWh nichtsdestotrotz nach knapp 5 Jahren amortisieren.